Brought to you by Dan Scotson.

Porosity in Materials

Pores are spaces in materials.

Pores are present in many materials, resulting in a material that is not fully dense. An example of pores are in sponges, where the gaps can hold water and help you wash dirty plates and dishes! However, pores are also found in other materials, including: ceramics, metals and polymers. Pores affect the behaviour of materials, for example, their electrical and  mechanical properties so it is important to understand the effect of pores on materials.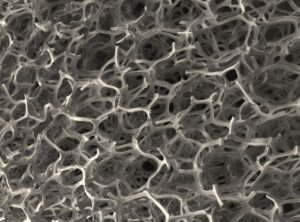

Purpose:

Pores can change the behaviour of a material. Therefore, as materials scientists, there is lots to investigate! The following points are especially interesting:

  1. How do pores affect material properties – is the material a better insulator of heat or is it easier to break with more pores?
  2. Can we control the number of pores and their size?
  3. Can we image the pores and understand where pores are located?

From this resource, the following intended learning outcomes are of interest:

  1. Describe materials where pores are present.
  2. Describe the relationship between porosity and stiffness.
  3. Propose a method of calculating the number of balls in a box.
  4. Explain how pores can influence the properties of materials.
  5. Evaluate whether pores are good or bad in these materials.

Audience:

The resources presented here were developed with accessibility to students from primary school age all the way up to undergraduate materials scientists. The level of delivery can therefore be adapted towards the required audience. For example, the maths involved in calculating the packing of the spheres can be adapted from a 2D geometry to a 3D geometry, dependent on the students’ confidence on shape and geometry topics.

The following topics areas are relevant to this resource and are defined in the National curriculum in England: mathematics programmes of study.

  • Primary (5-11 years)

Maths:

Recognise and name common 2-D and 3-D shapes, including: 2-D shapes [for example, rectangles (including squares), circles and triangles], 3-D shapes [for example, cuboids (including cubes), pyramids and spheres] and illustrating the named parts of circles, including radius, diameter and circumference and know that the diameter is twice the radius.

Science:

Uses of everyday materials. Find out how the shapes of solid objects made from some materials can be changed by squashing, bending, twisting and stretching. Describe the simple physical properties of a variety of everyday materials.

  • Secondary (12-16 years)

Maths:

Working mathematically and solving problems.

Extend and formalise their knowledge of ratio and proportion, including trigonometric ratios, in working with measures and geometry, and in working with proportional relations algebraically and graphically. Use the properties of faces, surfaces, edges and vertices of cubes, cuboids, prisms, cylinders, pyramids, cones and spheres to solve problems in 3-D.

Chemistry:

Properties of ceramics, polymers and composites (qualitative).

  • 16+

Maths:

Calculate the circumferences, surface areas and volumes of regular shapes.

Physics:

Mechanical properties of matter – Young’s modulus. Particle model and differences in arrangements, shape and density.

Chemistry:

Interpretation of the physical properties of materials in terms of structure and bonding.

Activity:

The following resources and activities were displayed at the Big Bang Fair, National Exhibition Centre (NEC), Birmingham in Summer 2023.

1) Ceramic manufacture: Four boxes demonstrating particle packing

The boxes are a model for particle packing, and contain different sizes and geometries of particles. The boxes are a good model for powder processing in manufacturing ceramics, although the spheres can also be thought of as atoms for atomic packing in crystal structures.

Four colourless boxes filled with different spheres and particle shapes. One box contains big spheres of the same size. One box contains smaller spheres of the same size. One box contains a mixture of big and small spheres. The fourth box contains an array of random shapes, including a Stegosaurus!
Four boxes illustrating particle packing of spheres and different shapes to attain the highest packing density.

Box 1: Big spheres, all the same size.

How many spheres can I fit in a box? How could I calculate how many spheres are in the box?

Box 2: Small spheres, all the same size.

If I use smaller spheres, can I fit more in? What about the total volume of the spheres and pores, does this change? (No, assuming a completely full box).

Box 3: A combination of the spheres from Box 1 and Box 2.

Can I achieve better packing if I use bigger and smaller spheres? Why is calculating the number of spheres now more difficult? (Fill the interstitial sites between the spheres – smaller balls can fit between bigger balls).

Box 4: A combination of different geometries.

What limits me using spheres? Particles can be different shapes. How could we fill all the gaps? (Apply understanding from Box 3 and Box 4 – Use different sizes and use different shapes!).

Further details on calculating packing fractions for particular crystal structures can be found here: PDF_Packing_Fraction_Calculations_20230617_DS.

2) Squash test (mechanical properties of porous materials)

Foam balls placed between Perspex discs show how pores affect the mechanical properties of ceramics. When there are less balls between the perspex discs, it is easier to squash the discs. This relates to the stiffness of materials as a function of porosity. Denser materials are stiffer.

Can you think of examples of stiff materials? Bone, Concrete, Ceramics. Can you think of examples of materials which are easy to stretch? Elastic, Polymers and Rubber.

Three foams balls in between two Perspex discs.
Model for describing the effect of porosity of the stiffness of materials. This model is representative of a porous ceramic as there are spaces for another three foam spheres.
Model for describing the effect of porosity of the stiffness of materials. This model is representative of a dense ceramic as there no spaces for more foam spheres.

Where is porosity important?

  • Polymers – Sponges and foams

Why do we want pores in these materials? How do we make the materials have pores? Introduce gases in manufacture.

  • Ceramics – Thermal Barrier Coatings for aeroplane jet-engines

Pores in these materials make these expand and contract more easily when heated to temperatures above 1200°C!

  • Metals – Additively Manufactured Components (3D printing)

Metals containing pores can make them easier to break. Taking images of pores can be done using X-ray computed tomography. You may know about these if someone has broken a bone and has had an X-ray scan.

Going further with this resource:

Common crystallography of metals

Metals have different crystal structures. The different crystal structures of metals affect the packing of metal ions. Some examples of different crystal structures include: Face-centered cubic (FCC) – Aluminium; Body-Centered Cubic (BCC) – Iron, and Hexagonal Close Packed (HCP) –  Zinc. Further examples of materials with particular crystal structures and materials containing porosity can be found here: PDF_Crystal_Structure_Examples_20230617_DS.

Further links:

The raw materials used to build and create these models and resources, demonstrated at Big Bang 2023, are detailed here: DM_Porosity_In_Materials_Resource_List_20230617_DS.

Further questions?

For more information, or questions regarding this activity, please contact us by using the ‘Contact Us’ form.

Written by..

Dan Scotson (check out Dan’s profile here )

You may also like

Will it Recycle?

Introduction Recycling plays a critical role in reducing waste, conserving natural resources, and minimizing environmental pollution. Educating students about recycling…

Protected: Discover Materials Resources and reporting (internal)

There is no excerpt because this is a protected post.

Teacher Newsletters – all issues

Near the start of every school term we publish a newsletter to highlight Materials Science and Engineering in the news,…